Genel Metot ile Çokgen Çizme Yöntemi (Yedigen çizeceğiz.)
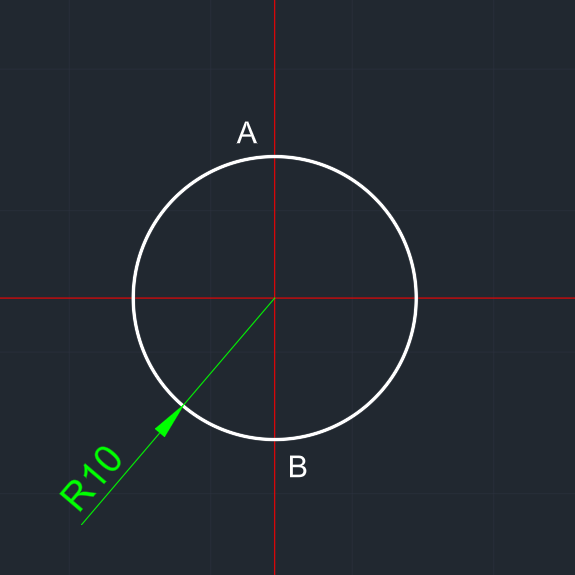
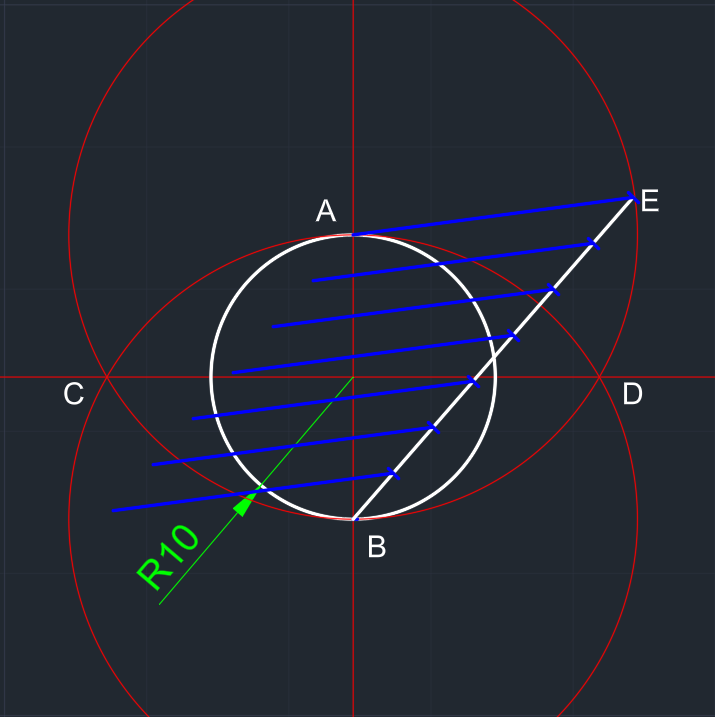
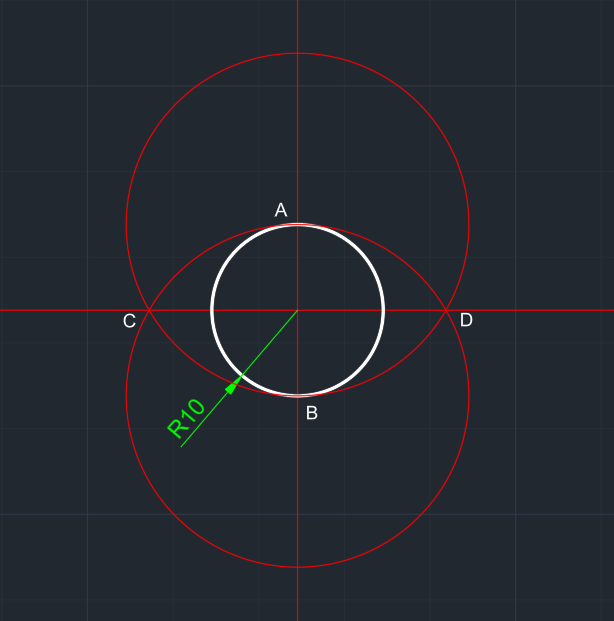
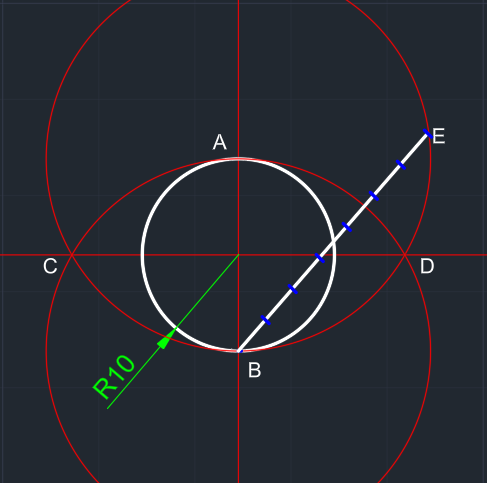
Dik eksenler çizilir.	Merkezden x (10) yarıçaplı bir çember çizilir. A ve B noktaları oluşur.	A ve B merkezli 2x yarıçaplı çemberler oluşturulur.	AB arasını 7'ye böleceğiz. Bunun için; B noktasından rastgele BE doğru parçası çizilir. Bu doğru parçası eşit şekilde 7'ye bölünür.
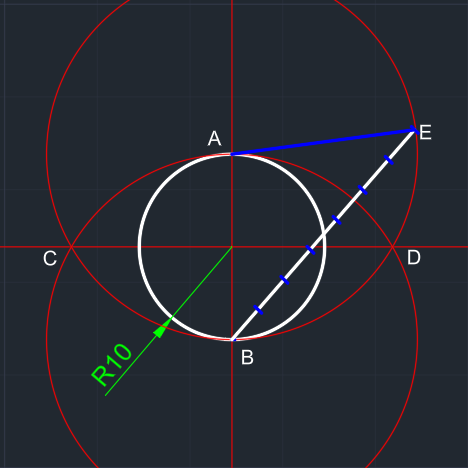
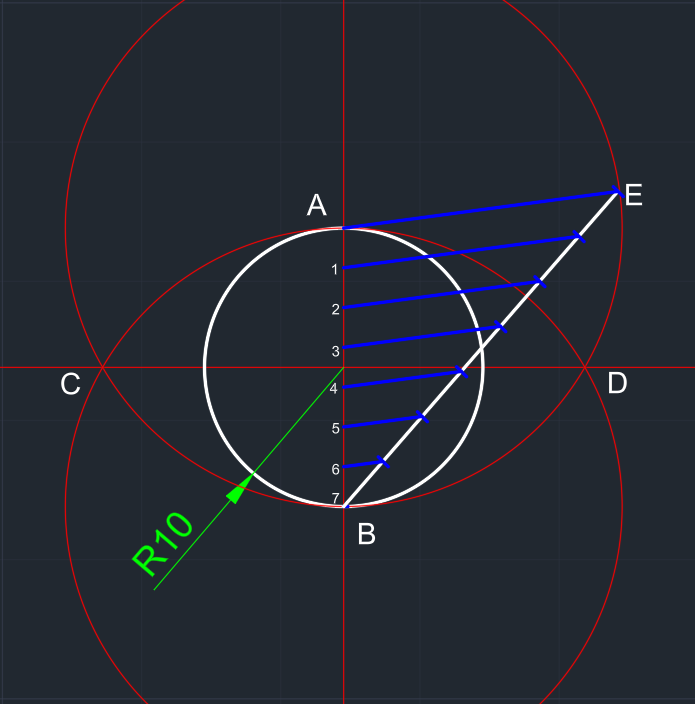
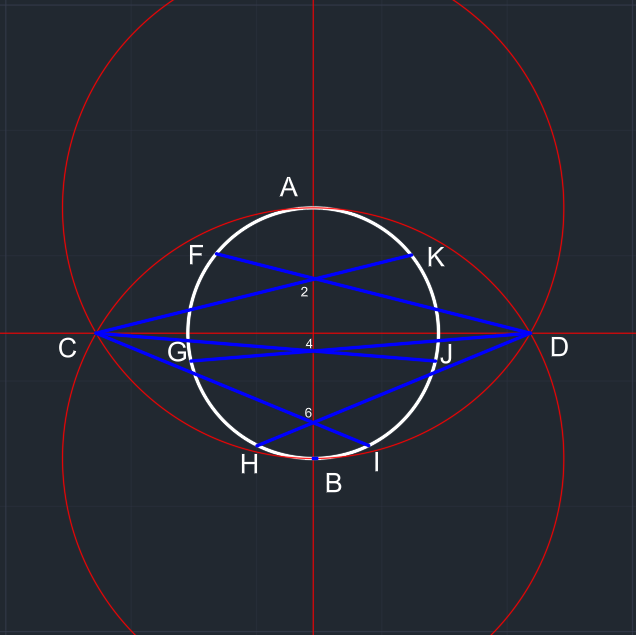
E ve A noktalarını birleştiren bir EA doğru parçası çizilir.	EA doğru parçası paralel bir şekilde BE üzerindeki noktalara kopyalanır.	Fazlalıklar silinir ve AB üzerindeki noktalar numaralandırılır.	C ve D noktalarından başlayıp 2, 4 ve 6 noktalarından geçip çemberin çevresine dayanan doğru parçaları çizilir. F, G, H, I, J ve K noktaları oluşur.
A, F, G, H, I, J ve K noktaları birleştirilerek AFGHIJK yedigeni oluşturulmuş olur.	Yardımcı çizgiler silinir.
Çember Yardımıyla Elips Çizme Yöntemi
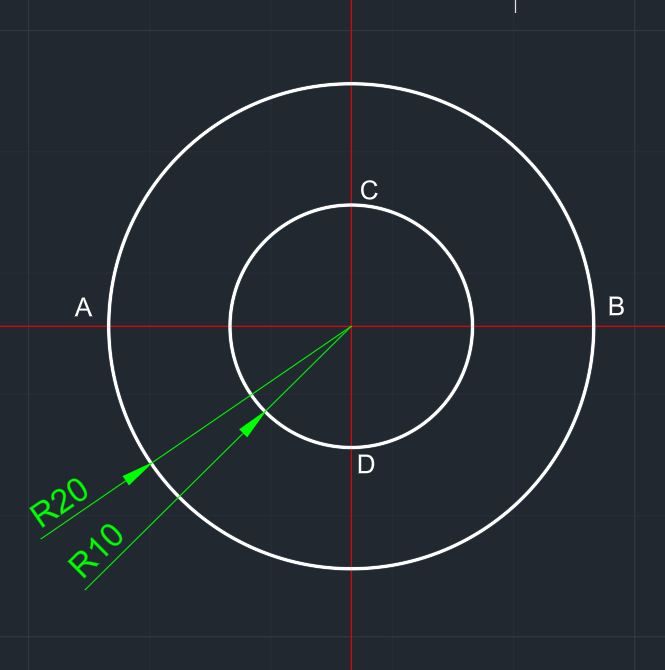
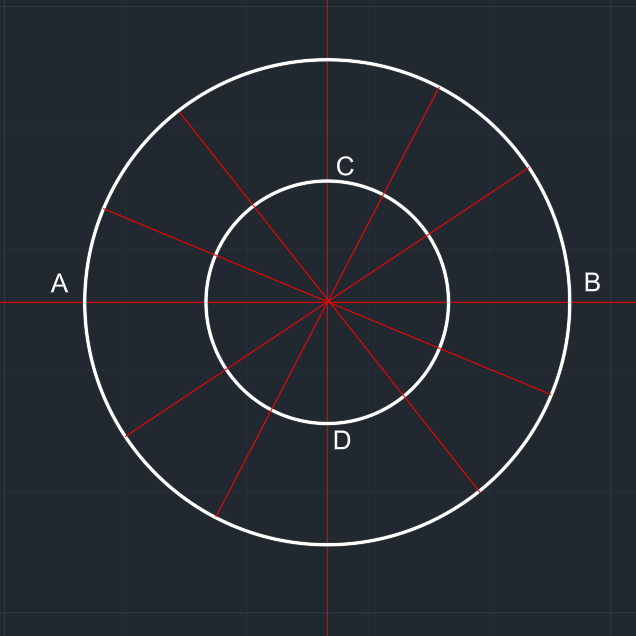
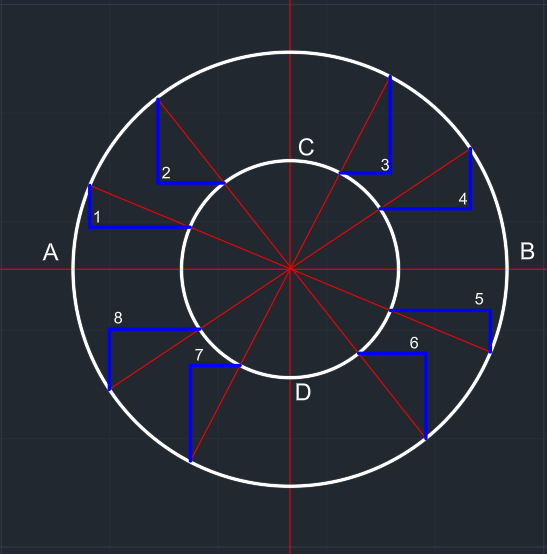
Dik eksenler çizilir.	Elipsin yatay ve dikey ölçülerine göre iki çember çizilir. A, B, C ve D noktaları belirlenir.	Merkezden geçen doğru parçalarıyla iki çember bölünür.	Bölme işleminden sonra çizgilerin çemberleri kesen noktalarından yatay ve dikey çizgiler çizilip kesişen noktalar numaralandırılır.
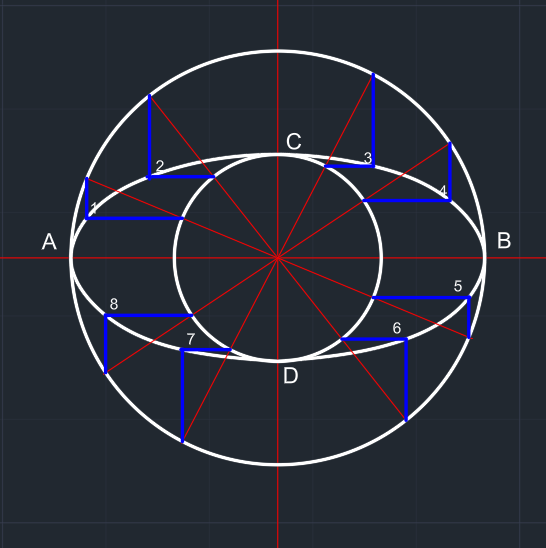
D, 7, 8, A, 1, 2, C, 3, 4, B, 5 ve 6 noktaları eğriler ile (Autocad'de: "Spline Fit" ile) birleştirilir.	Yardımcı çizgiler silinir.
Dikdörtgen Yardımıyla Elips Çizme Yöntemi
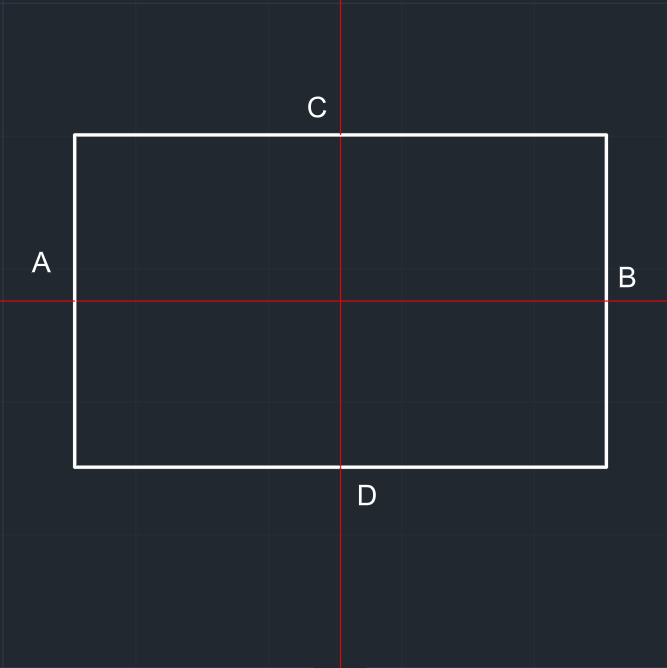
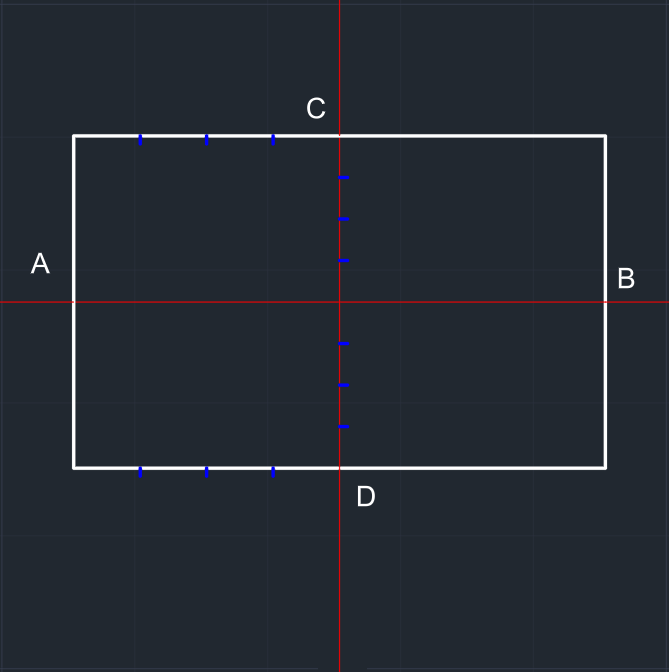
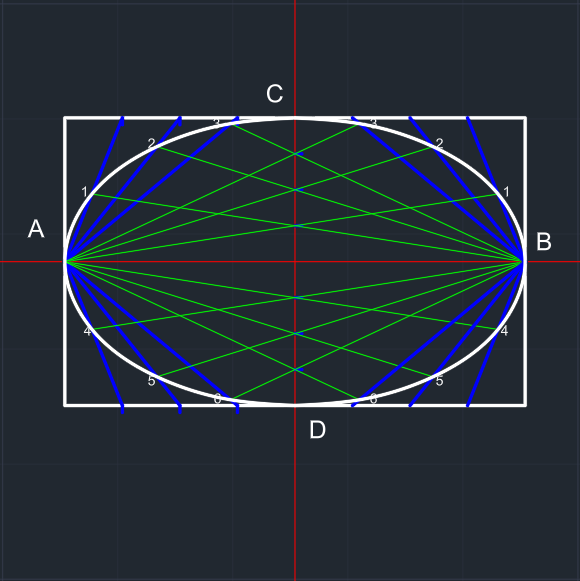
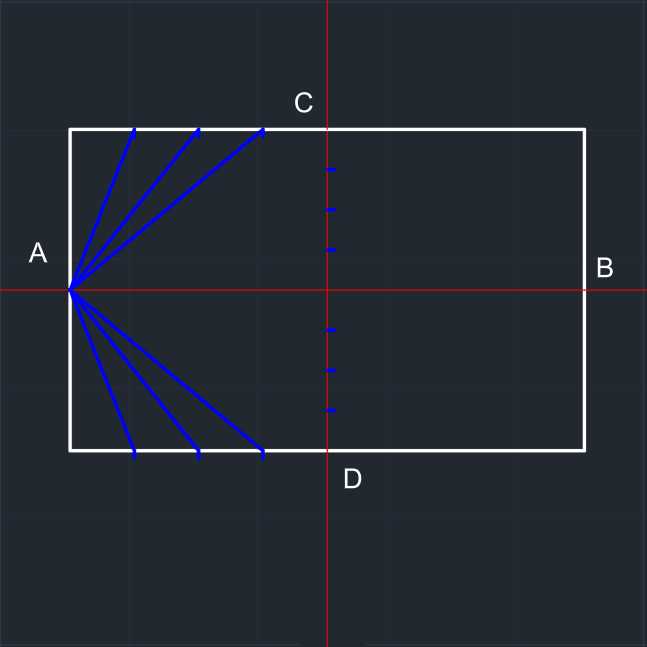
Dik eksenler çizilir.	Elipsin yatay ve dikey ölçülerine göre bir dikdörtgen çizilir. A, B, C ve D noktaları belirlenir.	Şekilde görülen dört çizim bölgesi üçe bölünür.	A noktasından dikdörtgen üzerindeki bölünen yerlere doğru parçaları çizilir.
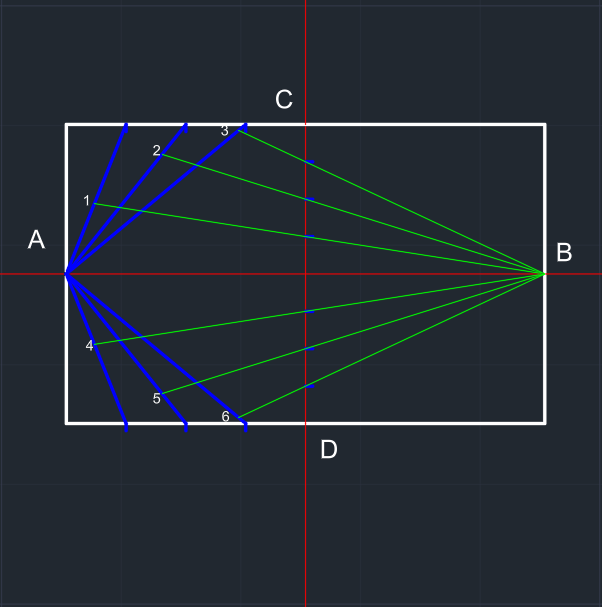
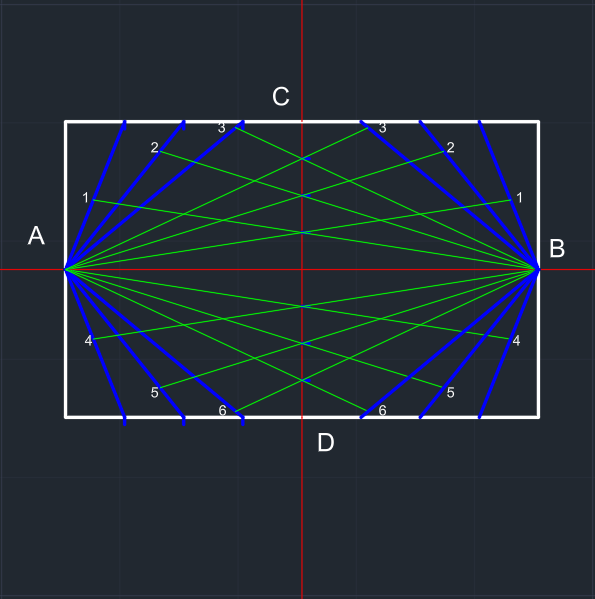
B noktasından eksen üzerindeki bölünen yerlerden geçip diğer doğru parçalarına uzanan doğru parçaları çizilir.	Bu işlem diğer tarafa da aynalanır. (Autocad'de: Mirror komutu)	Tüm noktalar Elips oluşturacak şekilde eğri (Spline Fit) ile birleştirilir.	Yardımcı çizgiler silinir.
İki Merkezli Spiral Çizme Yöntemi
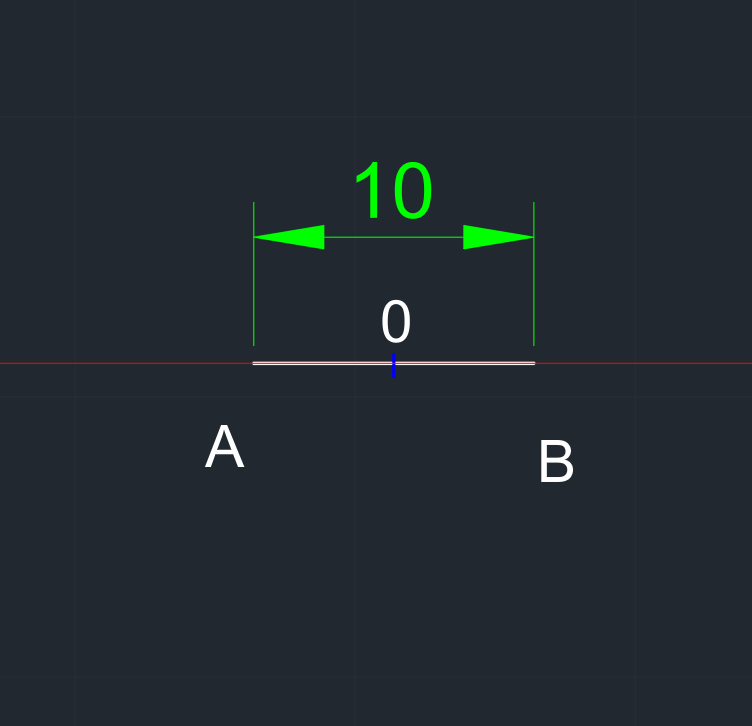
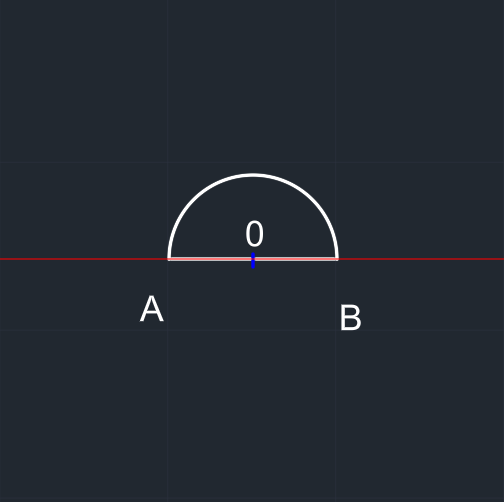
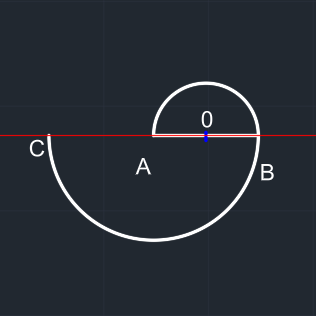
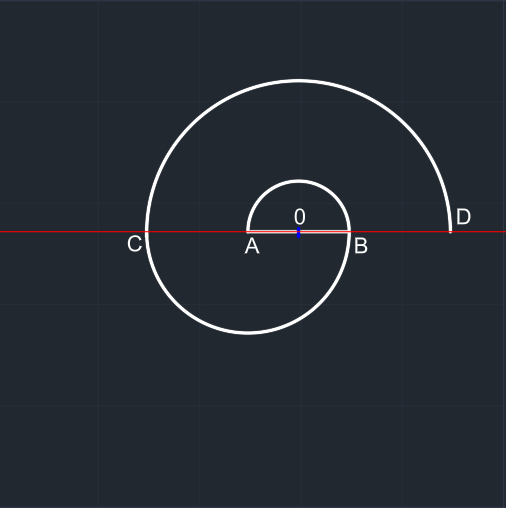
Yatay bir eksen çizilir.	x (10 birim) uzunluğunda AB doğru parçası çizilir. Orta noktası (0) işaretlenir.	0 merkezli x çaplı çember çizilir. Çember alttan budanır. Düzgün bir yarım çember elde edilir.	A merkezli 2x çaplı çember çizilir. Çember üstten budanır. Düzgün bir yarım çember elde edilir. C noktası oluşur.
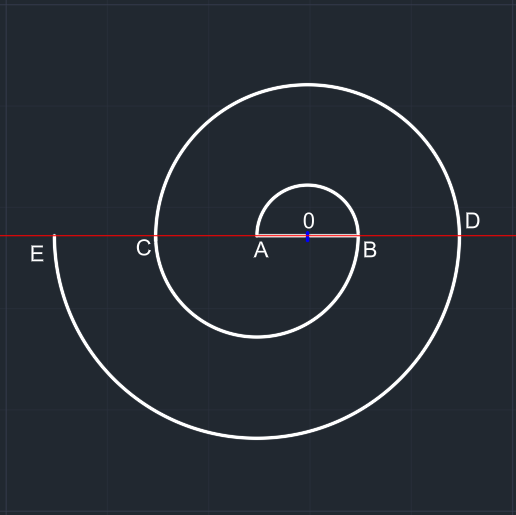
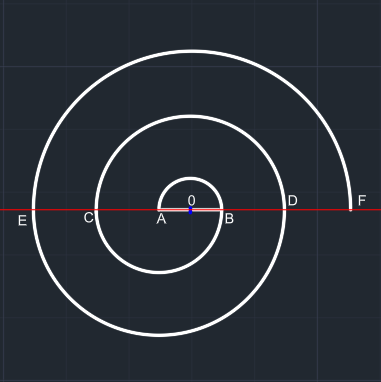
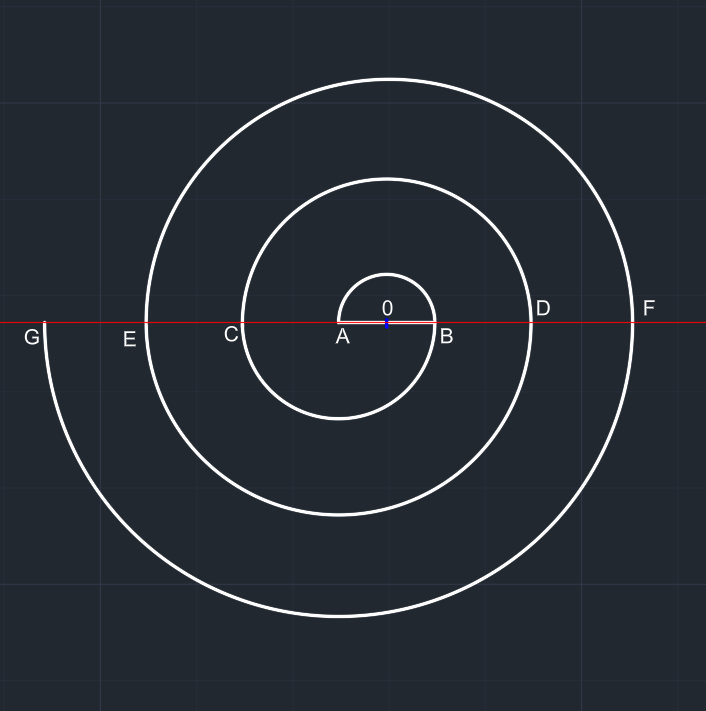
0 merkezli 3x çaplı çember çizilir. Çember alttan budanır. Düzgün bir yarım çember elde edilir. D noktası oluşur.	A merkezli 4x çaplı çember çizilir. Çember üstten budanır. Düzgün bir yarım çember elde edilir. E noktası oluşur.	0 merkezli 5x çaplı çember çizilir. Çember alttan budanır. Düzgün bir yarım çember elde edilir. F noktası oluşur.	A merkezli 6x çaplı çember çizilir. Çember üstten budanır. Düzgün bir yarım çember elde edilir. G noktası oluşur. Spiral hazır.
Kare ile Spiral Çizme Yöntemi
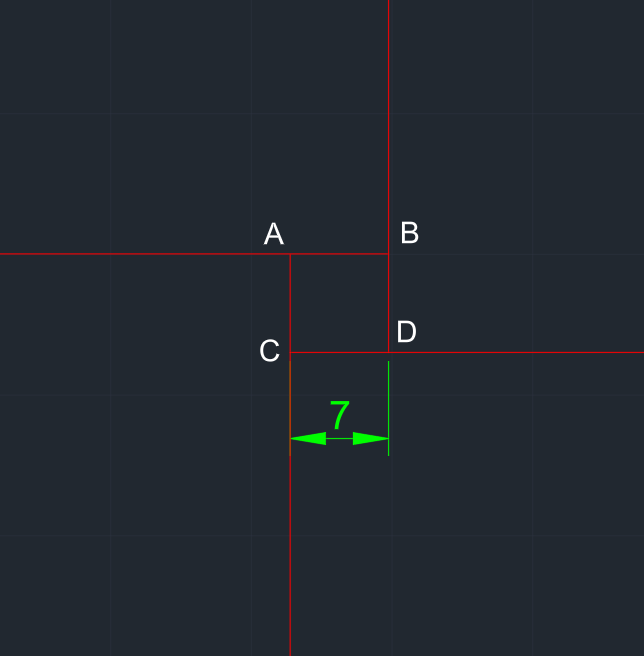
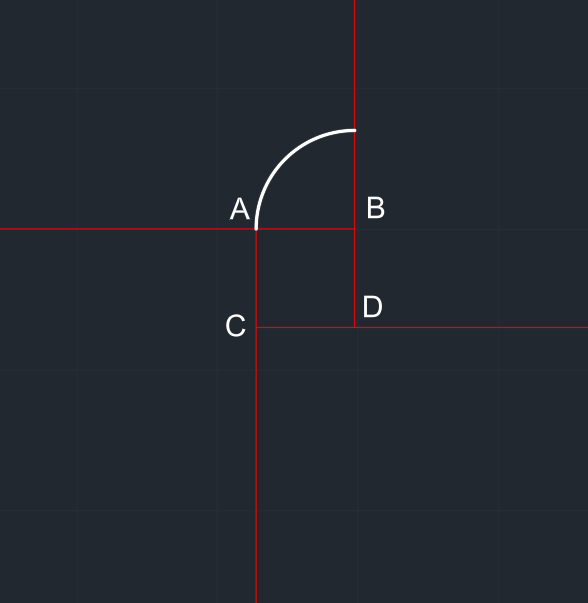
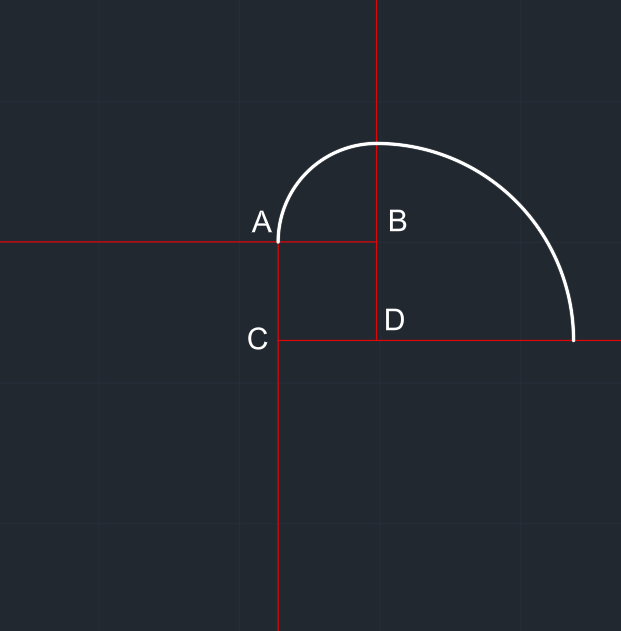
Ön Bilgi: Öncelikle koordinat düzlemindeki bölgeleri inceleyelim. Bu terimleri çizimde kullanacağız.	x (7) kenarlı bir kare çizilir. Karenin her kenarından doğru parçaları uzatılır. A, B, C ve D noktaları belirlenir.	B merkezli x yarıçaplı çember çizilir. Çember yalnızca 2. bölgesi kalacak şekilde budanır. Düzgün bir çeyrek çember elde edilir.	D merkezli 2x yarıçaplı çember çizilir. Çember yalnızca 1. bölgesi kalacak şekilde budanır. Düzgün bir çeyrek çember elde edilir.
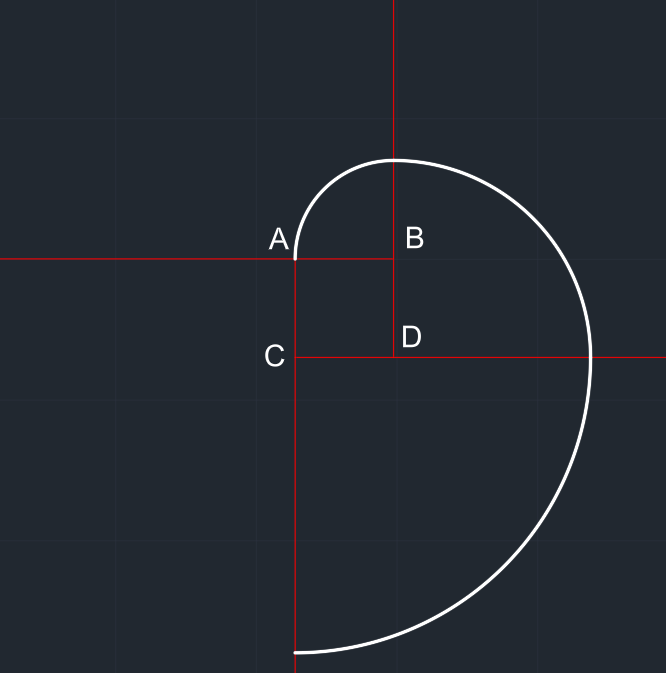
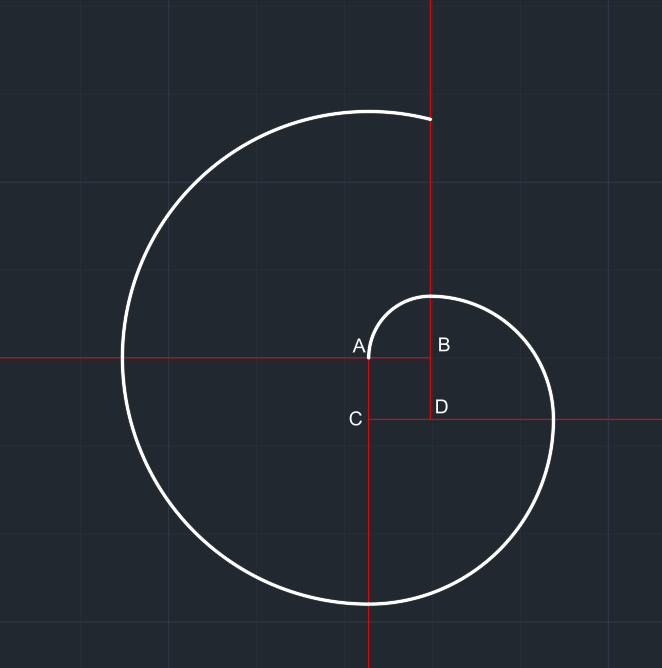
C merkezli 3x yarıçaplı çember çizilir. Çember yalnızca 4. bölgesi kalacak şekilde budanır. Düzgün bir çeyrek çember elde edilir.	A merkezli 4x yarıçaplı çember çizilir. Çember yalnızca 2. bölgesi kalacak şekilde budanır. Düzgün bir çeyrek çember elde edilir.
Arşimet Spirali Çizme Yöntemi
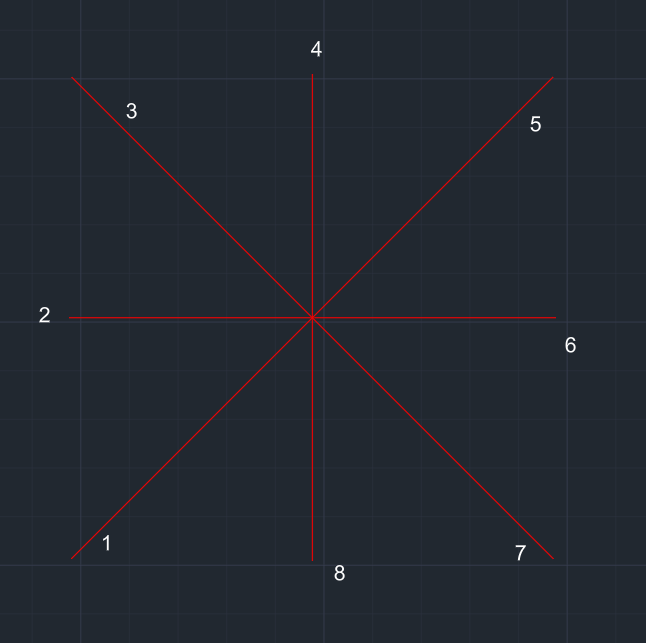
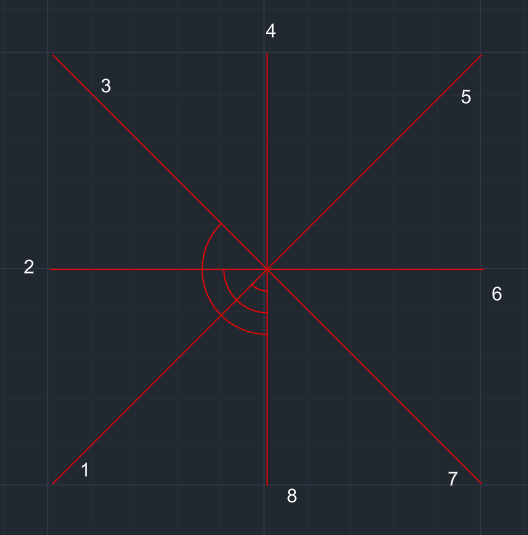
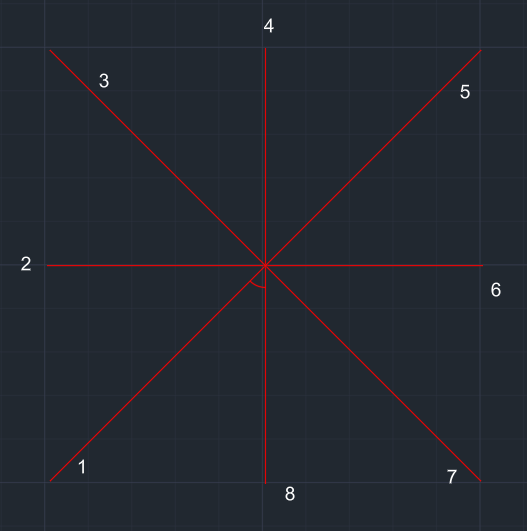
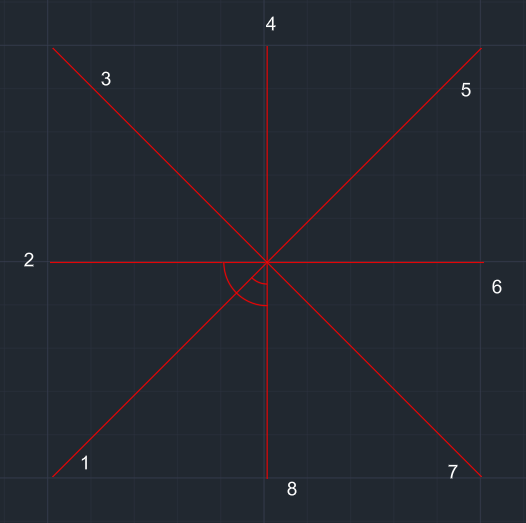
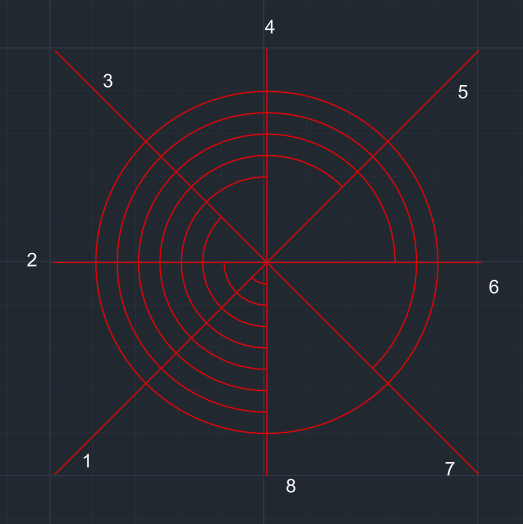
Merkezleri aynı dik ve çapraz eksenler çizilir. Her eksen numaralandırılır.	Merkezden x (5) yarıçaplı çember çizilir. Bu çemberin 1-8 arasında kalan bölümün dışı budanır.	Merkezden 2x yarıçaplı çember çizilir. Bu çemberin 2-1-8 arasında kalan bölümün dışı budanır.	Merkezden 3x yarıçaplı çember çizilir. Bu çemberin 3-2-1-8 arasında kalan bölümün dışı budanır.
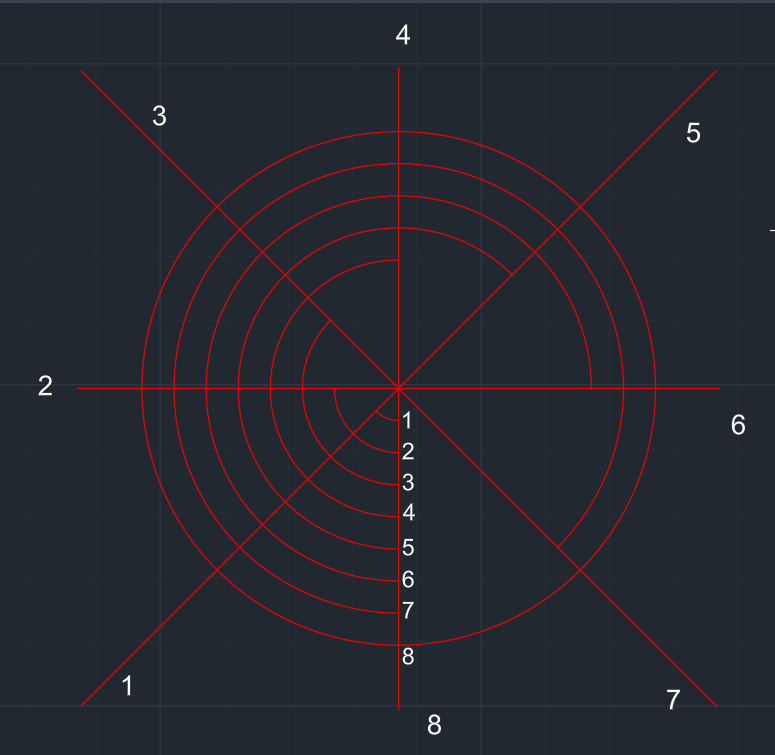
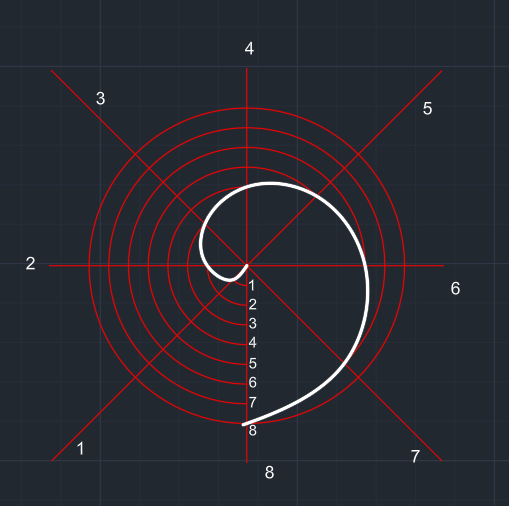
Bu işlem budanacak bölge kalmayana kadar yani tam bir çember çizene kadar devam eder.	Çemberlerin başlangıç yerleri numaralandırılır.	Merkezden başlayarak çemberlerin son noktaları eğri ile birleştirilir.	Arşimet spirali oluşur.
Evolvent Eğrisi Çizme Yöntemi
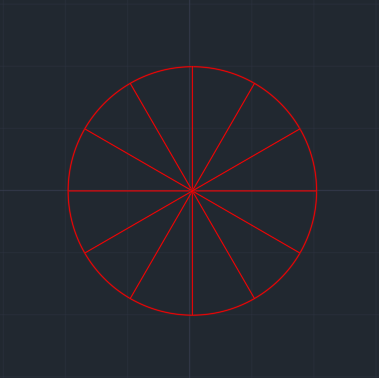
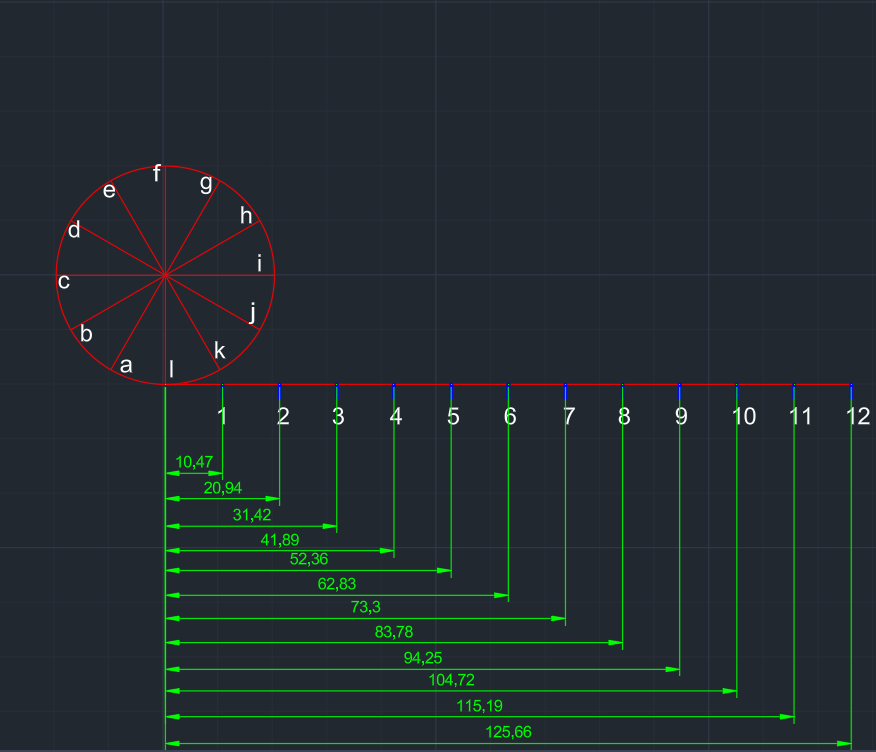
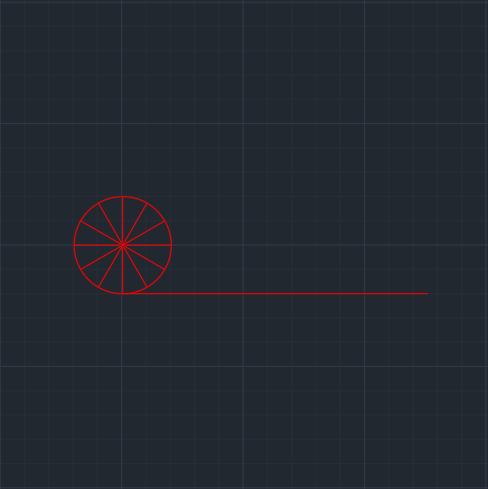
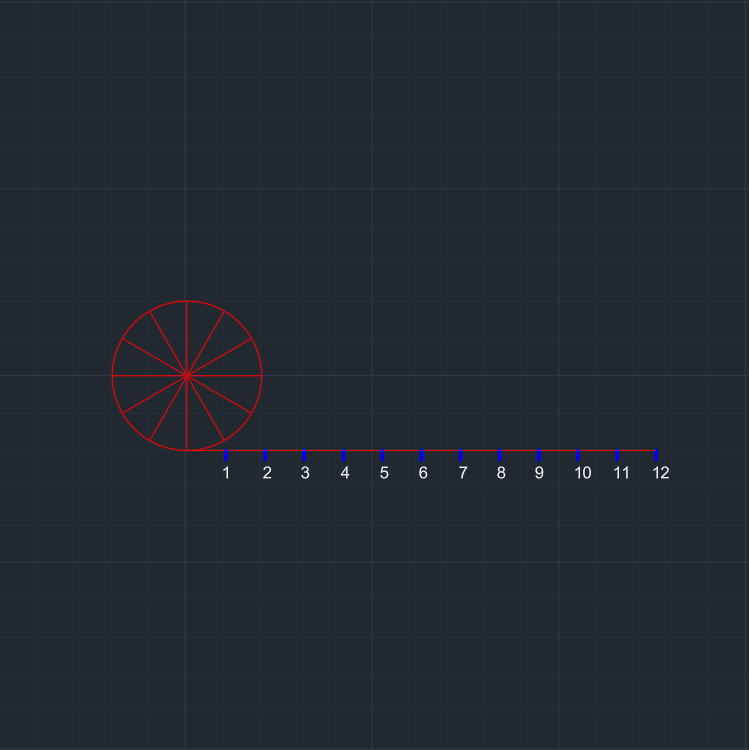
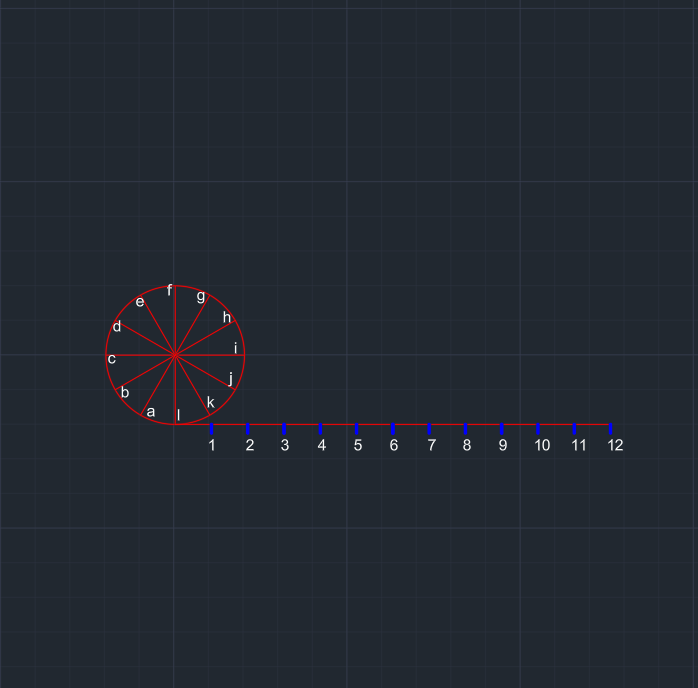
x (40) yarıçaplı bir çember çizilir. Çember y (12) eşit parçaya bölünür.	Çemberin tabanından yatay bir şekilde pi*x kadar bir doğru parçası çizilir.	Çizilen bu doğru parçası da y kadar eşit parçaya bölünür.	Çember içinde, doğru parçalarıyla çemberin kesiştiği noktalar saat 07.00 noktasından başlayacak şekilde harflendirilir.
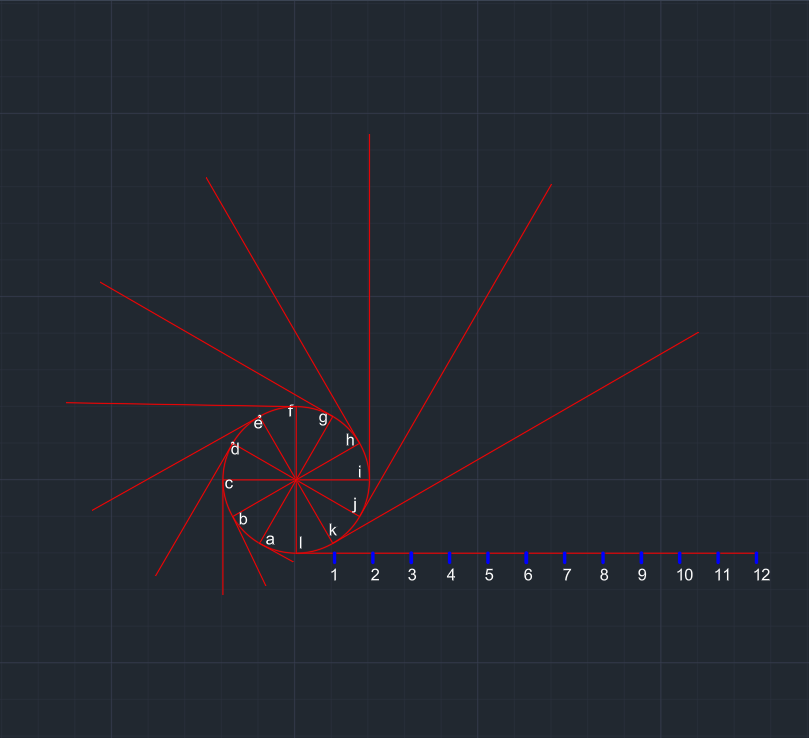
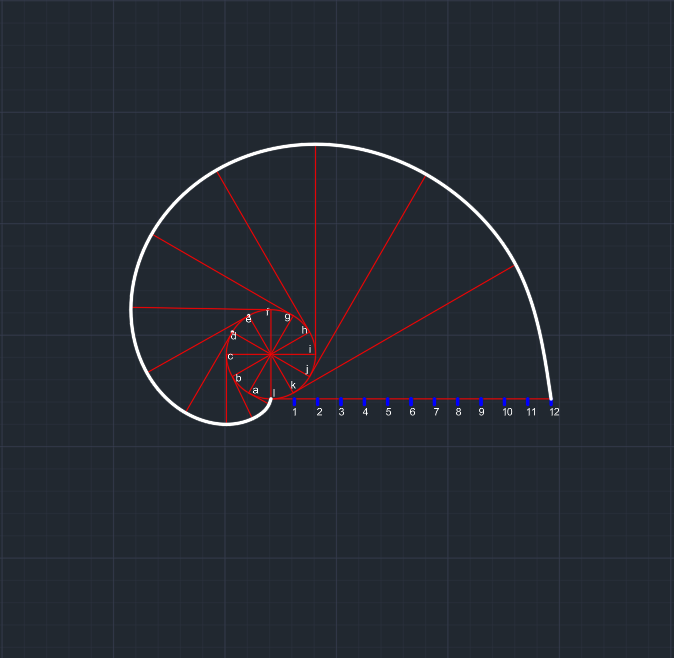
Doğru parçası üzerinde 0-1, 0-2, 0-3, ... 0-12 arası mesafeler ölçülür. Bu ölçümleri kullanacağız.	a noktasından 0-1, b noktasından 0-2, c noktasından 0-3, . . . k noktasından 0-11 ölçümü kadar teğet çizilir.	Sonra bu teğetlerin uçları l'den başlayarak birleştirilir.	Evolvent eğrisi oluşur.